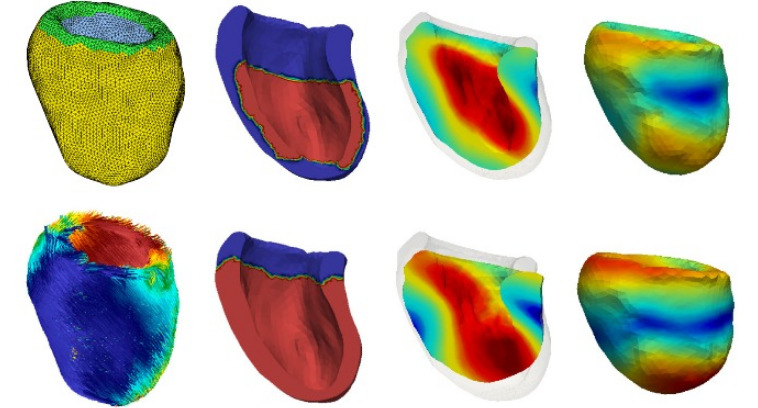
In particular his significant contributions to reduced basis methods impressed the prize committee. Reduced basis methods can be an effective tool for obtaining quickly solvable reduced order models of parametrized partial differential equation problems. With speedups that can reach several orders of magnitude, reduced basis methods enable high fidelity real-time simulations of complex systems and dramatically reduce the computational costs in many-query applications. Andrea Manzoni and his coworkers use these methods mainly for model reduction of fluid dynamics systems, in particular in the solution of the parametrized electromechanical model for heart dynamics.