Alberto
Barchielli (Politecnico di Milano): Modelli stocastici ed equazioni di Kolmogorov-Fokker-Planck
Le equazioni di Langevin sono equazioni di moto, del tipo delle equazioni di Hamilton, in cui appare una forza proporzionale ad un “rumore bianco”. La necessità di dare un significato matematico a queste equazioni portò allo sviluppo del “calcolo stocastico di Itô” e alla nozione di “equazione differenziale stocastica”. La soluzione di una di queste equazioni è un processo di Markov le cui probabilità di transizione sono legate a oggetti che soddisfano l' “equazione di Kolmogorov all'indietro”. Sotto ulteriori ipotesi, si ottiene l'esistenza delle densità di probabilità di transizione, e sono queste densità che soddisfano l'
“equazione di Kolmogorov in avanti”, o “equazione di Fokker-Planck”.
La presentazione matematica del calcolo stocastico e delle equazioni differenziali stocastiche richiederebbe troppo tempo per gli scopi di questa Scuola. Queste lezioni intendono solamente dare qualche idea euristica sul calcolo stocastico, per capire cosa sia un'equazione differenziale stocastica e come a partire da questa si ottenga l'equazione di Kolmogorov-Fokker-Plank.
Questi punti saranno illustrati introducendo esempi di equazioni di interesse per la fisica o, più in generale, per le scienze applicate.
Un semplice testo che contiene tutti gli argomenti di cui abbiamo bisogno è:
- Z. Schuss, Theory and Applications of Stochastic Differential Equations (Wiley, New York, 1980).
Una presentazione matematicamente accurata è data da:
- P. Baldi, Equazioni Differenziali Stocastiche e Applicazioni, Quaderni UMI 28 (Pitagora, Bologna, 2000).
Libri completamente dedicati alle applicazioni sono:
- H. Risken, The Fokker-Planck equation (Springer, Berlin, 1989);
- N.G. van Kampen, Stochastic Processes in Physics and Chemistry (Elsevier, Amsterdam 1992);
- C.W. Gardiner, Handbook of stochastic methods: for physics, chemistry and the natural sciences (Springer, Berlin, 1990).
Anthony Bloch (University of Michigan): Geometric
control theory and applications
The course will be based essentially on the
book:
- A. M. Bloch (with the collaboration of J. Baillieul,
P. Crouch, J. Marsden): Nonholonomic Mechanics and
Control.
Springer 2003.
Outline:
1.
Examples and mathematical preliminaries.
2. Geometric Mechanics
3.
Geometric Control
4. Nonholonomic Mechanics
5. Optimal Control and
sub-Riemannian geometry.
Bruno Franchi (Università di
Bologna): Geometria
indotta da campi vettoriali
Distanza di Carnot-Carathéodory associata a una famiglia di
campi vettoriali e applicazioni alle equazioni ellittiche degeneri
(disuguaglianza di Harnack e regolarità Hölderiana).
Proprietà
di duplicazione della misura delle palle e disuguaglianza di
Poincaré.
Spazi di Sobolev e spazi BV associati a metriche di
Carnot-Carathéodory.
Nozione di misura intrinseca di una sottovarietà
rispetto ad una metrica di Carnot-Carathéodory.
Indicazioni bibliografiche saranno
fornite durante il corso.
Ermanno Lanconelli (Università di
Bologna): Equazioni
differenziali lineari del second’ordine ipoellittiche:
Operatori di Hörmander su gruppi di Lie omogenei
1.
Le
equazioni di Kolmogorov e la condizione di Hörmander
Nel 1934 Kolmogorov
introdusse una classe di equazioni paraboliche degeneri le cui soluzioni
positive rappresentano la densità di probabilità di sistemi fisici con
fissati gradi di libertà. Per il prototipo di queste equazioni Kolmogorov
costruì una esplicita soluzione fondamentale di classe 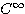 fuori dai poli. Il corrispondente operatore differenziale è quindi
ipoellittico. In questa prima parte del corso, si presenta la
costruzione delle soluzione fondamentale di Kolmogorov, e si prova che la
sua esistenza segue da una condizione di “rango massimo” per un'opportuna
algebra di Lie di campi vettoriali (questa condizione, se formulata
per gli operatori differenziali “somme di quadrati”, diventa la celebre
condizione di ipoellitticità di Hörmander). Si riconosce poi che l'algebra
di Lie che “governa” l'operatore di Kolmogorov, è l'algebra di un gruppo di
Lie omogeneo, rispetto alle cui traslazioni a sinistra e dilatazioni,
l'operatore stesso è invariante. Questa parte del corso è contenuta
nella nota:
fuori dai poli. Il corrispondente operatore differenziale è quindi
ipoellittico. In questa prima parte del corso, si presenta la
costruzione delle soluzione fondamentale di Kolmogorov, e si prova che la
sua esistenza segue da una condizione di “rango massimo” per un'opportuna
algebra di Lie di campi vettoriali (questa condizione, se formulata
per gli operatori differenziali “somme di quadrati”, diventa la celebre
condizione di ipoellitticità di Hörmander). Si riconosce poi che l'algebra
di Lie che “governa” l'operatore di Kolmogorov, è l'algebra di un gruppo di
Lie omogeneo, rispetto alle cui traslazioni a sinistra e dilatazioni,
l'operatore stesso è invariante. Questa parte del corso è contenuta
nella nota:
- E. Lanconelli, S.Polidoro:
On a class of
hypoelliptic evolution operators, Rend . Sem. Mat. Univ. Pol. Torino, 52
(1994),29-63.
2.
Gruppi di Lie omogenei in 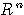 : una introduzione
“self-contained”
: una introduzione
“self-contained”
In questa parte del corso si presentano i
primi elementi della teoria dei gruppi di Lie omogenei in 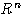 . La
presentazione è “self-contained”, rivolta a non specialisti, e richiede
soltanto conoscenze elementari del calcolo differenziale per funzioni
vettoriali di piu' variabili reali. Saranno disponibili note
scritte.
. La
presentazione è “self-contained”, rivolta a non specialisti, e richiede
soltanto conoscenze elementari del calcolo differenziale per funzioni
vettoriali di piu' variabili reali. Saranno disponibili note
scritte.
3. Operatori di Hörmander invarianti su gruppi omogenei:
(i) Soluzione fondamentale;
(ii)
Disuguaglianza di Harnack;
(iii) Teoremi di
Liouville;
(iv) Teoria del potenziale.
Quest'ultima parte del corso
è incentrarata sulle due note seguenti:
- A.E.Kogoj, E.Lanconelli: An
invariant Harnack inequality for a class of hypoelliptic ultraparabolic
equations, Mediterr. J. of Math, to appear.
- A.E.Kogoj, E.Lanconelli: One-side Liouville Theorems for a class of
hypoelliptic ultraparabolic
equations, Contemporary Mathematics, to appear.
Marco
Peloso (Politecnico di Torino): Problemi geometrici in più variabili complesse e campi vettoriali:
Analisi
del Kohn-Laplaciano
su varietà di Cauchy-Riemann
Di fondamentale importanza in analisi di più
variabili complesse sono le equazioni di Cauchy-Riemann su domini, e le equazioni
di Cauchy-Riemann tangenziali su varietà immerse. Queste equazioni
vengono generalmente studiate introducendo un problema di valori al bordo,
il cosiddetto problema 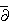 -Neumann e un operatore sulla varietà,
il Laplaciano di Kohn, rispettivamente. Nell'analisi della regolarità
di tali problemi ed operatori risulta di fondamentale importanza la condizione
dei campi di Hörmander, o un suo opportuno analogo. In questo breve
ciclo di lezioni si studierà l'operatore di Kohn-Laplace
-Neumann e un operatore sulla varietà,
il Laplaciano di Kohn, rispettivamente. Nell'analisi della regolarità
di tali problemi ed operatori risulta di fondamentale importanza la condizione
dei campi di Hörmander, o un suo opportuno analogo. In questo breve
ciclo di lezioni si studierà l'operatore di Kohn-Laplace 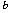 sulle varietà di Cauchy-Riemann e si mostrerà come proprietà
geometriche della varietà possano garantire la validità della
condizione di Hörmander e quindi una certa regolarità delle soluzioni
dell'equazione
sulle varietà di Cauchy-Riemann e si mostrerà come proprietà
geometriche della varietà possano garantire la validità della
condizione di Hörmander e quindi una certa regolarità delle soluzioni
dell'equazione 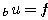 . Si indicheranno applicazioni di questi
risultati. Infine, tempo permettendo, si introdurrà il problema di
valori al bordo
. Si indicheranno applicazioni di questi
risultati. Infine, tempo permettendo, si introdurrà il problema di
valori al bordo 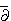 -Neumann.
-Neumann.
Programma (di
massima)
- Introduzione alle varietà CR, la forma di Levi
- Il complesso
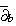 e il Kohn-Laplaciano
e il Kohn-Laplaciano 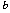
- Alcuni esempi notevoli: il gruppo di Heisenberg e le varietà
CR quadratiche
- Ipoellitticità, subelliticità e risolubilità per
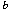
- Alcune applicazioni: il proiettore di Cauchy-Szegö, spazi di
Hardy, estendibilità di forme
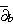 -chiuse
-chiuse
- Stime
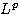 per
per 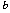
- Introduzione al problema
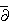 -Neumann (cenni)
-Neumann (cenni)
Bibliografia (parziale)
- S-C. Chen, M-C. Shaw, Partial Differential Equations in
Several Complex Variables, Studies in Advanced Mathematics
19, AMS/International Press, Providence 2001.
- A. Boggess, CR manifolds and the tangential Cauchy-Riemann complex,
Studies in Advanced Mathmatics, CRC Press, Boca Raton, 1991.
- J.B. Folland, E. M. Stein, Estimates for the
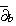 complex
and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27
(1974), 429-522.
complex
and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27
(1974), 429-522.
- M.M. Peloso, F. Ricci, Analysis of the Kohn-Laplacian on quadratic
CR manifolds, J. Funct. Anal. 203 (2003), 321-355.
- L.P. Rosthchild, E.M. Stein, Hypoelliptic differential operators on
nilpotent Lie groups, Acta Math. 137 (1976), 247-320.
 fuori dai poli. Il corrispondente operatore differenziale è quindi
ipoellittico. In questa prima parte del corso, si presenta la
costruzione delle soluzione fondamentale di Kolmogorov, e si prova che la
sua esistenza segue da una condizione di “rango massimo” per un'opportuna
algebra di Lie di campi vettoriali (questa condizione, se formulata
per gli operatori differenziali “somme di quadrati”, diventa la celebre
condizione di ipoellitticità di Hörmander). Si riconosce poi che l'algebra
di Lie che “governa” l'operatore di Kolmogorov, è l'algebra di un gruppo di
Lie omogeneo, rispetto alle cui traslazioni a sinistra e dilatazioni,
l'operatore stesso è invariante. Questa parte del corso è contenuta
nella nota:
fuori dai poli. Il corrispondente operatore differenziale è quindi
ipoellittico. In questa prima parte del corso, si presenta la
costruzione delle soluzione fondamentale di Kolmogorov, e si prova che la
sua esistenza segue da una condizione di “rango massimo” per un'opportuna
algebra di Lie di campi vettoriali (questa condizione, se formulata
per gli operatori differenziali “somme di quadrati”, diventa la celebre
condizione di ipoellitticità di Hörmander). Si riconosce poi che l'algebra
di Lie che “governa” l'operatore di Kolmogorov, è l'algebra di un gruppo di
Lie omogeneo, rispetto alle cui traslazioni a sinistra e dilatazioni,
l'operatore stesso è invariante. Questa parte del corso è contenuta
nella nota: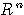 : una introduzione
“self-contained”
: una introduzione
“self-contained”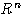 . La
presentazione è “self-contained”, rivolta a non specialisti, e richiede
soltanto conoscenze elementari del calcolo differenziale per funzioni
vettoriali di piu' variabili reali. Saranno disponibili note
scritte.
. La
presentazione è “self-contained”, rivolta a non specialisti, e richiede
soltanto conoscenze elementari del calcolo differenziale per funzioni
vettoriali di piu' variabili reali. Saranno disponibili note
scritte. -Neumann e un operatore sulla varietà,
il Laplaciano di Kohn, rispettivamente. Nell'analisi della regolarità
di tali problemi ed operatori risulta di fondamentale importanza la condizione
dei campi di Hörmander, o un suo opportuno analogo. In questo breve
ciclo di lezioni si studierà l'operatore di Kohn-Laplace
-Neumann e un operatore sulla varietà,
il Laplaciano di Kohn, rispettivamente. Nell'analisi della regolarità
di tali problemi ed operatori risulta di fondamentale importanza la condizione
dei campi di Hörmander, o un suo opportuno analogo. In questo breve
ciclo di lezioni si studierà l'operatore di Kohn-Laplace 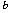 sulle varietà di Cauchy-Riemann e si mostrerà come proprietà
geometriche della varietà possano garantire la validità della
condizione di Hörmander e quindi una certa regolarità delle soluzioni
dell'equazione
sulle varietà di Cauchy-Riemann e si mostrerà come proprietà
geometriche della varietà possano garantire la validità della
condizione di Hörmander e quindi una certa regolarità delle soluzioni
dell'equazione 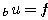 . Si indicheranno applicazioni di questi
risultati. Infine, tempo permettendo, si introdurrà il problema di
valori al bordo
. Si indicheranno applicazioni di questi
risultati. Infine, tempo permettendo, si introdurrà il problema di
valori al bordo 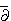 -Neumann.
-Neumann. 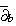 e il Kohn-Laplaciano
e il Kohn-Laplaciano 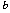
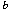
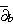 -chiuse
-chiuse 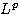 per
per 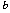
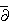 -Neumann (cenni)
-Neumann (cenni) 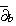 complex
and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27
(1974), 429-522.
complex
and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27
(1974), 429-522.